More Geometry and Trig

In the geometry and trig chapter we learned stuff that are very useful for writing games, and I have used something from that chapter in almost all 2D games I have made. In this chapter you'll learn things that are sometimes useful.

This chapter assumes that you have read the first geometry and trig chapter.

Pythagorean Theorem

Let's say that we have a triangle with a quarter-turn corner, and its sides are $a$, $b$ and $c$ where $c$ is the longest side. In the picture at right, the small square at the bottom-right corner means that we're talking about a quarter-turn corner. This works with any triangle that has a quarter-turn corner:

$$\begin{align}a^2 + b^2 = c^2\end{align}$$

We'll prove this soon. Note that $c$ must be the longest side of the triangle, but it doesn't matter which side is $a$ and which is $b$ because $b^2+a^2 = a^2+b^2$.

The Pythagorean theorem has many important applications:

$$\begin{align}\sqrt{a^2 + b^2} = \sqrt{c^2} = |c| = c\end{align}$$

The last step assumes $c \ge 0$, but that's not a problem because a triangle with a negative side length doesn't make much sense. Many programming languages have a hypot() function that works like this:

$$\begin{align}\text{hypot}(a,b) = \sqrt{a^2 + b^2}\end{align}$$

It's also possible to solve for other sides, e.g. $b = \sqrt{c^2 - a^2}$.

It doesn't matter which point is which:

$$\begin{align}\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} &= \sqrt{\bigl(-(x_1-x_2)\bigr)^2 + \bigl(-(y_1-y_2)\bigr)^2} \\ &= \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\end{align}$$

Here I used the $a-b=-(b-a)$ and $(-x)^2=x^2$ formulas from the basics page.

This also works if $x$ or $y$ is negative or if they are both negative; the negativeness doesn't matter because $(-x)^2 = x^2$ with any $x$.

Exercise

Use unit circle trig and the Pythagorean theorem to prove that $\sin^2(\theta)+\cos^2(\theta)=1$ with any $\theta$.

Pythagorean Theorem Proof

Now we have looked into a bunch of ways to use the Pythagorean theorem, but let's prove that it actually works. This is a well-known proof, and I like it because it's simple.

Let's start by arranging 4 abc triangles like this:

Handy thing: $(a+b)^2=a^2+2ab+b^2$

Proof using $(a+b)c=ac+bc$:

$$\begin{align}& \ (a+b)^2 \\ =&\ (a+b)(a+b) \\ =&\ a(a+b)+b(a+b) \\ =&\ aa+ab+ba+bb \\ =&\ a^2+2ab+b^2\end{align}$$

We can calculate the total area of the above square in a couple different ways using some basic area stuff:

We must get the same area with both ways, so we get this:

$$\begin{align}(a+b)(a+b) &= c^2 + 4\frac{ab}{2} \\ (a+b)^2 &= c^2 + \frac{4}{2} ab \\ a^2 \rcancel{+ 2ab} + b^2 &= c^2 \rcancel{+ 2ab} \\ a^2 + b^2 &= c^2\end{align}$$

Exercise

Draw an $a+b$ by $a+b$ square, and use areas to derive the handy thing we used above.

Cartesian to Polar Coordinates

We know that every point on the xy plane can be represented with $(x,y)$ coordinates, but we can also represent every point with a distance from $(0,0)$ and an angle:

$$\begin{align}\left\{\begin{array}{l} x = r\cos(\theta) \\ y = r\sin(\theta) \\ \end{array}\right.\end{align}$$

Fancy words that make you sound like a mathematician: the $(x,y)$ form is known as Cartesian coordinates, and the $(r,\theta)$ form is called polar coordinates.

If we know $r$ and $\theta$, finding $x$ and $y$ is simple as plugging them in to the equations above. But how about figuring out $r$ and $\theta$ from $x$ and $y$? This is useful if you have written a game using $x$ and $y$ coordinates, but you want to also do something that's easier with polar coordinates.

We can use Pythagorean theorem to figure out $r$:

$$\begin{align}r = \text{hypot}(x, y) = \sqrt{x^2+y^2}\end{align}$$

Rewriting $\theta$ in terms of $x$ and $y$ so that all corner cases are covered is a bit more complicated, so programmers defined a function just for that:

$$\begin{align}\theta = \text{atan2}(y,x)\end{align}$$

Note that $y$ goes before $x$; getting this mixed up gives wrong angles.

The atan2 function was originally a thing in programming languages only, but nowadays at least some non-programming-related math articles on Wikipedia use it as well. The 2 at the end of atan2 means that it takes two arguments unlike atan, and in the next section I'll explain what atan is.

Triangle Trig

The word "trigonometry" means triangle something, and trig functions like $\sin$ and $\cos$ can be also defined in a triangle with a quarter-turn corner. We can get those definitions from our circle stuff by drawing a triangle under the red $(x,y)$ point like in the image at right.

Something interesting happens:

$$\begin{align}\frac x r = \frac{r\cos(\theta)}{r} = \cos(\theta) \\ \frac y r = \frac{r\sin(\theta)}{r} = \sin(\theta)\end{align}$$

More fancy words: if we have a triangle with a quarter-turn corner, the opposite side of a corner means the side opposite of that corner, and the adjacent side means the side that is not opposite or the hypotenuse.

Now we are ready to define $\sin$ and $\cos$ with nothing but a quarter-turn-cornered triangle. We'll also define a third function called $\tan$ that we haven't used before.

$$\begin{align}\sin(\theta) &= \frac{\text{opposite}}{\text{hypotenuse}} \\ \cos(\theta) &= \frac{\text{adjacent}}{\text{hypotenuse}} \\ \tan(\theta) &= \frac{\text{opposite}}{\text{adjacent}}\end{align}$$

Note that this stuff only makes sense for $0 < \theta < \frac \tau 4$; otherwise we'd need to think about triangles with negative side lengths, and circles in xy plane are a much handier way to handle that.

If we apply the $\tan$ definition to our circle pic above, we get this:

$$\begin{align}\tan(\theta) &= \frac y x \\ \theta &= \arctan\left(\frac y x\right)\end{align}$$

Here $\arctan$ means the inverse of $\tan$, and most programming languages have an atan function that computes arctan. However, earlier we did $\theta = \text{atan2}(y,x)$. Here are some things that can go wrong with $\arctan(\frac y x)$:

Here's our conclusion: atan2 is good because it handles corner cases. However, you can use plain atan if you know that the angle is between $-\frac \tau 4$ and $\frac \tau 4$; this corresponds to $x > 0$ in Cartesian to polar conversion.

Exercise

Use triangle trig to prove that $\tan(\theta)=\dfrac{\sin(\theta)}{\cos(\theta)}$. Even though triangle trig is limited to $0 < \theta < \frac \tau 4$, the above formula can be used to define $\tan(\theta)$ for any $\theta$ as long as $\cos(\theta) \ne 0$.

Notation Notes

sin2(x)

In this tutorial, I'll often write $\sin^2(x)$ when I mean $(\sin(x))^2$, and I also do $\cos^2(x)$ and $\tan^2(x)$. The $\sin^2(x)$ notation looks like really weird nonsense at first, but there are a couple reasons why I use it:

The comic is from here.

sec, csc, cot... head explodes

The only trig functions used in this tutorial are sin, cos, tan and their inverse functions, but if you read math stuff from e.g. Wikipedia, you may come across these functions:

$$\begin{align}\sec(\theta) &= \frac{1}{\cos(\theta)} \\ \csc(\theta) &= \frac{1}{\sin(\theta)} \\ \cot(\theta) &= \frac{\cos(\theta)}{\sin(\theta)} = \frac{1}{\tan(\theta)}\end{align}$$

I think it's just way more clear to write $\frac{1}{\sin(x)}$ than $\csc(x)$. This tutorial uses $\tan$ even though it's just $\frac{\sin(x)}{\cos(x)}$ because it can be quite handy, and it also lets you understand why the awesome atan2 function was named atan2.

Triangle Angle Sum

This section uses the Greek alpha, beta and gamma letters $\alpha$, $\beta$ and $\gamma$ to represent angles. Don't get confused – they are just letters, like a, b, c or $\theta$.

In the above picture, every red angle is a half turn minus blue angle, and we know that half turn is $\tau/2$ radians. Let's start at the little arrow at bottom and move along the edges clockwise until we arrive at the arrow again. The red angles represent how much we need to turn at each corner, and those turns are $\frac\tau2-a$, $\frac\tau2-b$ and $\frac\tau2-c$.

But in total we turned a full turn or $\tau$ radians:

$$\begin{align}\tau &= \left(\frac\tau2-\alpha\right) + \left(\frac\tau2-\beta\right) + \left(\frac\tau2-\gamma\right) \\ &= \frac\tau2 - \alpha + \frac\tau2 - \beta + \frac\tau2 - \gamma \\ &= 3\frac\tau2 -\alpha-\beta-\gamma \\ \alpha+\beta+\gamma &= \frac 3 2 \tau - \tau = \frac \tau 2\end{align}$$

So if we add together all the angles of a triangle we get a half turn. This works with any triangle. We'll find this useful later.

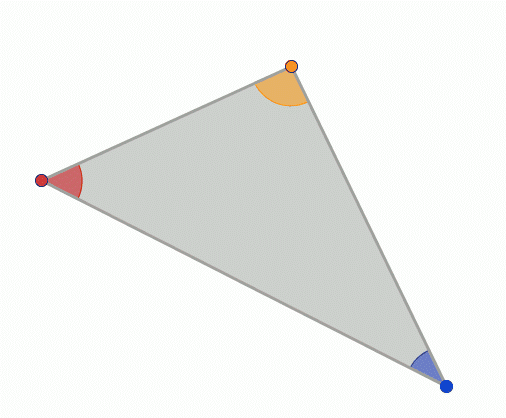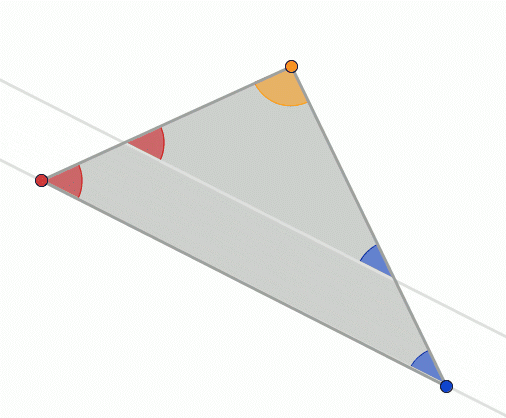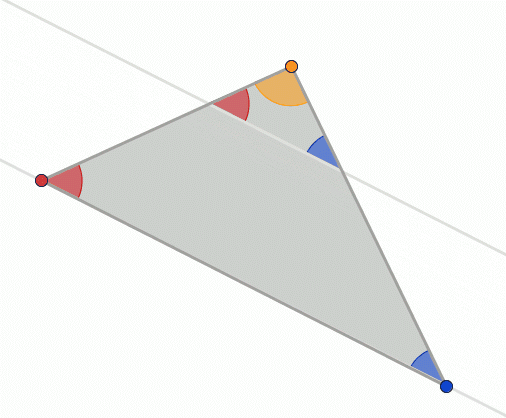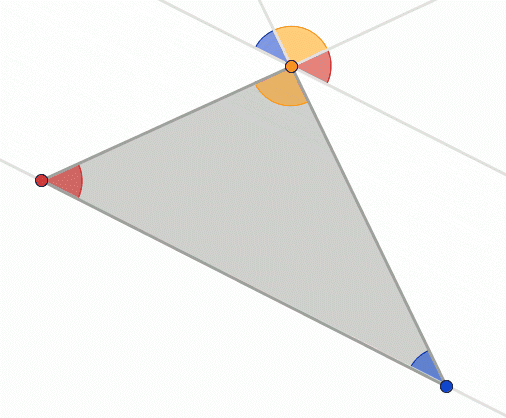
The animation comes from here.

Why is cosine called cosine?

Let's have a look at the triangle at right. We know that it's a triangle, so the sum of the angles must be $\frac \tau 2$ (see above).

$$\begin{align}\alpha + \beta + \frac \tau 4 &= \frac \tau 2 \\ \blue \beta &= \frac \tau 2 - \frac \tau 4 - \alpha = \blue{\frac \tau 4 - \alpha}\end{align}$$

We also know these things:

$$\begin{align}\cos(\alpha) &= \frac{\alpha\text{'s adjacent}}{\text{hypotenuse}} = \frac a c \\ \sin(\beta) &= \frac{\beta \text{'s opposite}}{\text{hypotenuse}} = \frac a c\end{align}$$

Setting these equal and plugging in $\blue\beta=\blue{\frac\tau4-\alpha}$ gives this:

$$\begin{align}\cos(\alpha) &= \sin\left(\blue{\frac \tau 4 - \alpha}\right)\end{align}$$

Only angles between $0$ and $\frac \tau 4$ make sense as triangle corners, but this actually works with any $\alpha$.

The angle $\frac\tau4-\alpha$ is also known as the complement angle because when added together, the angles "complete" to $\frac\tau4$:

$$\begin{align}\left( \frac \tau 4 - \alpha \right) + \alpha = \frac \tau 4\end{align}$$

Actually "cos" is short for "complement sine" as it's just the sine of the complement.

Rest of this chapter assumes that you know derivatives.

Derivative of Sine

Let's draw an angle $\theta$ and a change $\Delta\theta$ in the unit circle. We'll assume that $\theta$ is in radians, so it's an arc length on the unit circle.

Here the black ∢ signs mean an angle. It looks a lot like a circle arc, but in this case we are only interested in the angles, not circle arcs with radius 1.

Anyway, the orange line is parallel with the $x$ axis, and that's why we have two equal angles like the arrows in the picture show. But we know that the lower angle is simply $\theta + \Delta\theta$, so the upper angle is also $\theta + \Delta\theta$.

Let's zoom on the blue area:

That's quite a mess! Make sure you fully understand it before continuing.

Unfortunately we need to make the mess even messier by defining new variables $\alpha$ and $h$ like this:

The $h$ is just the difference of the $y$ coordinates.

$$\begin{align}h = \sin(\theta+\Delta\theta)-\sin(\theta)\end{align}$$

Next we need to figure out what $\alpha$ is. We can rotate from the orange line all the way to the blue $\Delta\theta$ line in a couple different ways: we can do $\theta+\Delta\theta+\frac \tau 4$ where $\frac \tau 4$ is the tiny corner square, or we can do $\frac \tau 4 + \alpha$ where $\frac \tau 4$ is the bigger square. Let's set those equal:

$$\begin{align}\theta + \Delta\theta + \rcancel{\frac \tau 4} &= \rcancel{\frac \tau 4} + \alpha \\ \theta + \Delta\theta &= \alpha\end{align}$$

The blue area looks kind of like a triangle, so we can apply triangle trig to it, but it's not a perfect triangle so we'll use $\approx$ instead of $=$.

$$\begin{align}\cos(\alpha) &\approx \frac{\text{adjacent}}{\text{hypotenuse}} \\ \cos(\alpha) &\approx \frac{h}{\Delta\theta} \\ \cos(\theta+\Delta\theta) &\approx \frac{\sin(\theta+\Delta\theta)-\sin(\theta)}{\Delta\theta}\end{align}$$

This looks kind of like a definition of derivative already! The above picture seems to be quite precise, and if we make $\Delta\theta$ even smaller, the errors go away:

$$\begin{align}\lim_{\Delta\theta\to0}\cos(\theta+\Delta\theta) &= \lim_{\Delta\theta\to0}\frac{\sin(\theta+\Delta\theta)-\sin(\theta)}{\Delta\theta} \\ \cos(\theta) &= \frac{d}{d\theta}\sin(\theta)\end{align}$$

This proof is based on a picture that makes sense only for $0 < \theta < \frac \tau 4$, but the same derivative rule works with any $\theta$. Note that $\theta$ must be in radians.

Exercise

Find the derivative of cosine similarly with a unit circle. The below proof uses $\frac{d}{d\theta}\sin(\theta)=\cos(\theta)$ instead of using unit circle stuff again, so you can't cheat by scrolling down.

Derivative of Cosine

Now we know that $\frac{d}{d\theta} \sin(\theta) = \cos(\theta)$ and $\cos(\theta) = \sin(\tau/4 - \theta)$, so we can do this easily, but we'll need the chain rule.

$$\begin{align}\frac{d}{d\theta} \cos(\theta) &= \frac{d}{d\theta}\sin\Bigl(\underbrace{\frac\tau4 - \theta}_{\text{inner stuff}}\Bigr) \\ &= \cos\Bigl(\frac\tau4 - \theta\Bigr) \cdot \frac{d}{d\theta}\Bigl(\frac\tau4 - \theta\Bigr) \\ &= \sin\biggl(\frac\tau4 - \Bigl(\frac\tau4 - \theta\Bigr)\biggr) \cdot (0-1) \\ &= \sin\Bigl(\rcancel{\frac\tau4} \rcancel{- \frac\tau4} + \theta\Bigr) \cdot (-1) \\ &= -\sin(\theta)\end{align}$$

Let's check the result with graphs:

We know that $\frac{d}{d\theta} \sin(\theta) = \cos(\theta)$, so finding the derivative moved the graph left. Similarly, the $-\sin(\theta)$ graph is the $\cos(\theta)$ graph shifted left.

Derivative of Tangent

Here $\tan^2(\theta)$ means $(\tan(\theta))^2$ as explained here.

We need a few things that we have proved earlier. These things are from this chapter:

We also need these things from the more derivatives chapter:

Let's do this.

$$\begin{align}\frac{d}{d\theta}\tan(\theta) &= \frac{d}{d\theta} \left( \frac{\blue{\sin(\theta)}}{\green{\cos(\theta)}} \right) \\ &= \frac{d}{d\theta} \left( \blue{\sin(\theta)} \green{\frac{1}{\cos(\theta)}} \right) \\ &= \Bigl(\frac{d}{d\theta}\blue{\sin(\theta)}\Bigr)\green{\frac{1}{\cos(\theta)}} + \blue{\sin(\theta)}\biggl(\frac{d}{d\theta}\Bigl( \green{\frac{1}{\maroon{\cos(\theta)}}}\Bigr)\biggr) \\ &= \rcancel{\cos(\theta)}\frac{1}{\rcancel{\cos(\theta)}} + \sin(\theta)\biggl( \frac{-1}{\maroon{\cos}^2\maroon{(\theta)}}\biggl(\frac{d}{d\theta}\maroon{\cos(\theta)}\biggr)\biggr) \\ &= 1 + \sin(\theta)\frac{-1}{\cos^2(\theta)}(-\sin(\theta)) \\ &= 1 + (-1)(-1)\frac{\sin^2(\theta)}{\cos^2(\theta)} \\ &= 1 + \left(\frac{\sin(\theta)}{\cos(\theta)}\right)^2 \\ &= 1 + \tan^2(\theta)\end{align}$$

That was a mess, but we're done! In fact, there's a formula for finding the derivative of $\frac{\blue{f(x)}}{\green{g(x)}}$ that we could just plug stuff into, but it's not very different from rewriting as $\blue{f(x)}\green{\frac{1}{g(x)}}$ and then taking the derivative like we just did.

If we're clever, we can rewrite this a bit differently:

$$\begin{align}1+\tan^2(\theta) &= \frac{\cos^2(\theta)}{\green{\cos^2(\theta)}} + \frac{\sin^2(\theta)}{\green{\cos^2(\theta)}} \\ &= \frac{\purple{\cos^2(\theta)+\sin^2(\theta)}}{\green{\cos^2(\theta)}} \\ &= \frac{1}{\cos^2(\theta)}\end{align}$$

Both of these answers can be useful; the first one is nice because the derivative is written entirely in terms of the original function, and the second one e.g. simplifies nicely under a square root.